このサイトでは、大学数学の色んな問題を提示してます. 今回は、位相の概念を理解する上でのその１を解説します.

この記事では、最終的に位相空間へどの様な過程で抽象化してくのかをいくつかの記事に分けて解説していきます。全く位相空間について理解できないなど、しっかり復習したい方は必見です。

その１～何記事までなるか分かりませんが記事の最後に続の記事のリンクを張っていますので続けて見ていくことをオススメ致します。

それではまず、位相空間への道のりについてどのような過程で進んでいくのか解説していきます。

“目次”

“位相空間への道のり”
1-1.ユークリッド距離関数の定義
1-2.距離空間の定義
1-3.距離空間上での収束の定義
1-4.距離空間上での連続の定義
1-5.距離空間の基本的な例
次回

“位相空間への道のり”

まずは、位相空間への道のりの上で必要な事柄をいくつか紹介し、その上でどのように進めていくか簡単に説明していきます。

第１:まず、位相空間を考える重要な理由として、収束や連続を抽象的に記述したいという理由があります。
その上で、今まで考えてきた\(\mathbb{R}^n:=\){\((x_1,…,x_n)|x_1,…,x_n \in \mathbb{R}\)} \((n次ユークリッド空間)\)に対して、\(“d”\)という距離の概念を導入することにより、収束や連続を考えることが可能になります。
そして、導入したものを、ユークリッド距離空間といい、\((\mathbb{R}^n,d)\)と書きます。

第２:次に、もう少し\((\mathbb{R}^n,d)\)を一般化していきたいと考えたとき、集合を\(\mathbb{R}^n\)に限定しなくてもっと一般的な集合\(X\)を導入することを考えます。
しかしこの集合\(X\)上で距離を定めるとき、もちろんユークリッド距離空間のような距離を定めれるとは限りません(どのような集合か分からないから)。
そこでいくつかの条件を付け加えることによって、その集合\(X\)の距離を定めることが出来ます(その条件については、この記事を書いていく中で説明していきます)。
そしてこの\((X,d)\)を距離空間といいます

第３:ここからさらに距離空間\((X,d)\)の性質である、開集合、内点、内部、閉集合、触点、閉包などの性質を導き出すことが出来ます。

第４:これらより、大まかに説明すると、距離空間\((X,d)\)の各性質(開集合、内部、閉集合、…)を要素に入れた概念を位相と言い\(“\mathcal{O}”\)で表し、その組\((X,\mathcal{O})\)を位相空間という

では、これらを順序立てて何記事かに分けて位相空間までの道のり、そしてその具体例などを含めながら説明していきます.

1-1.ユークリッド距離関数の定義

では、ユークリッド距離関数の定義を書いていきます。

定義

\(\mathbb{R}^n:=\){\((x_1,…,x_n)|x_1,…,x_n \in \mathbb{R}\)}　\((n次ユークリッド空間)\)

\(x\)\(=(x_1,…,x_n)\), \(y\)\(=(y_1,…,y_n)\) \(\in \mathbb{R}\) に対して、

\(d(x,y):=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+・・・+(x_n-y_n)^2}\)

(ただし、\(d(x,y)\geq 0\))と定める.

このとき、　

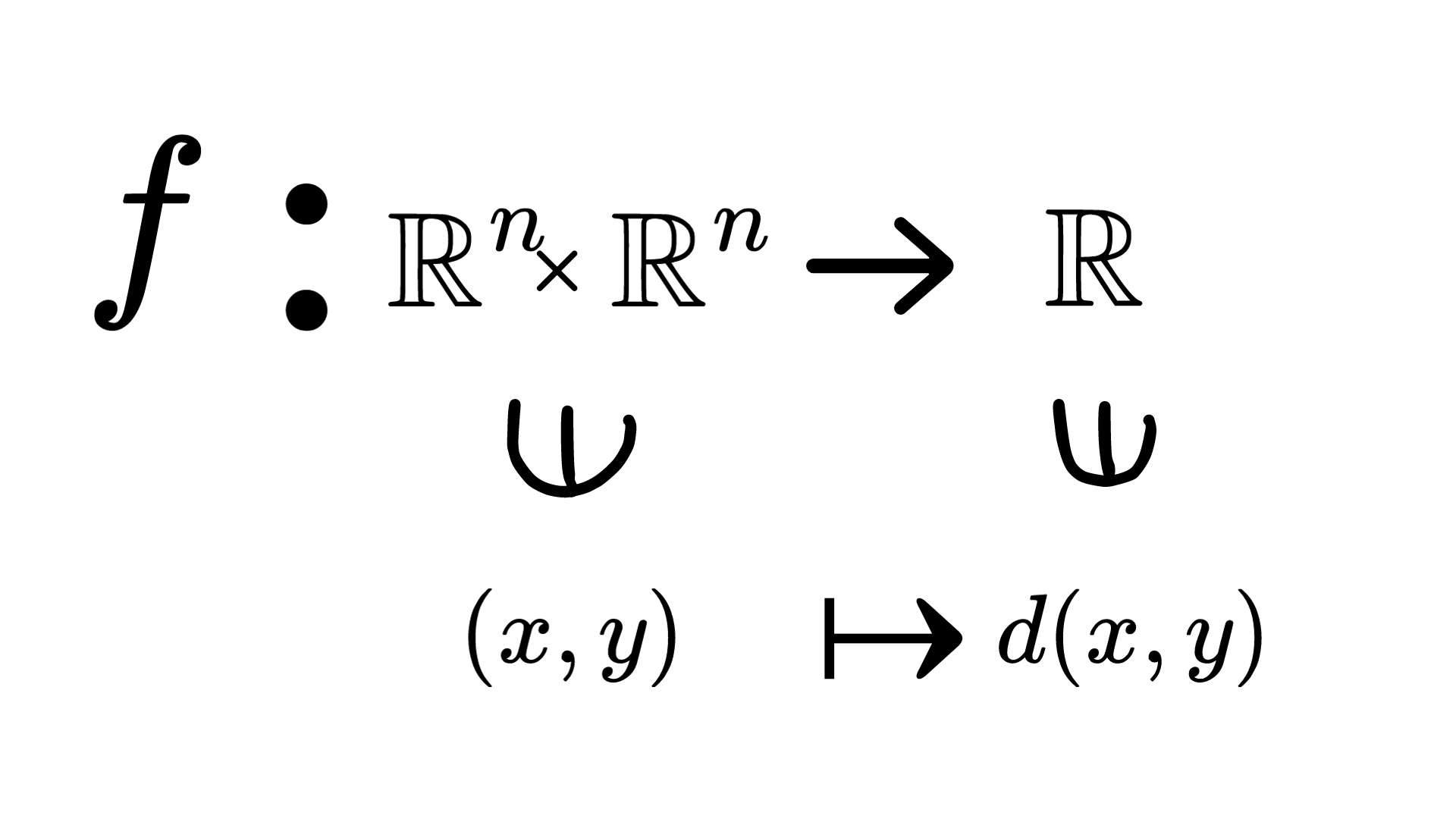
をユークリッド距離関数と呼ぶ

つまり、\(\mathbb{R}^nのみでなく、dという距離の概念を導入した(\mathbb{R}^n,d)を考える\)

そして、この\((\mathbb{R}^n,d)\)をユークリッド距離空間という

そして次では、この\((\mathbb{R}^n,d)\);ユークリッド距離空間をさらに一般化した\((X,d)\);距離空間について解説します。つまり、集合\(\mathbb{R}^n\)を\(X\)という一般の集合へ拡張した概念についても成り立つのかを考えます。

1-2.距離空間の定義

では距離空間の定義を見ていきましょう

定義

\(X : 空でない集合\)
\(関数dについて\)

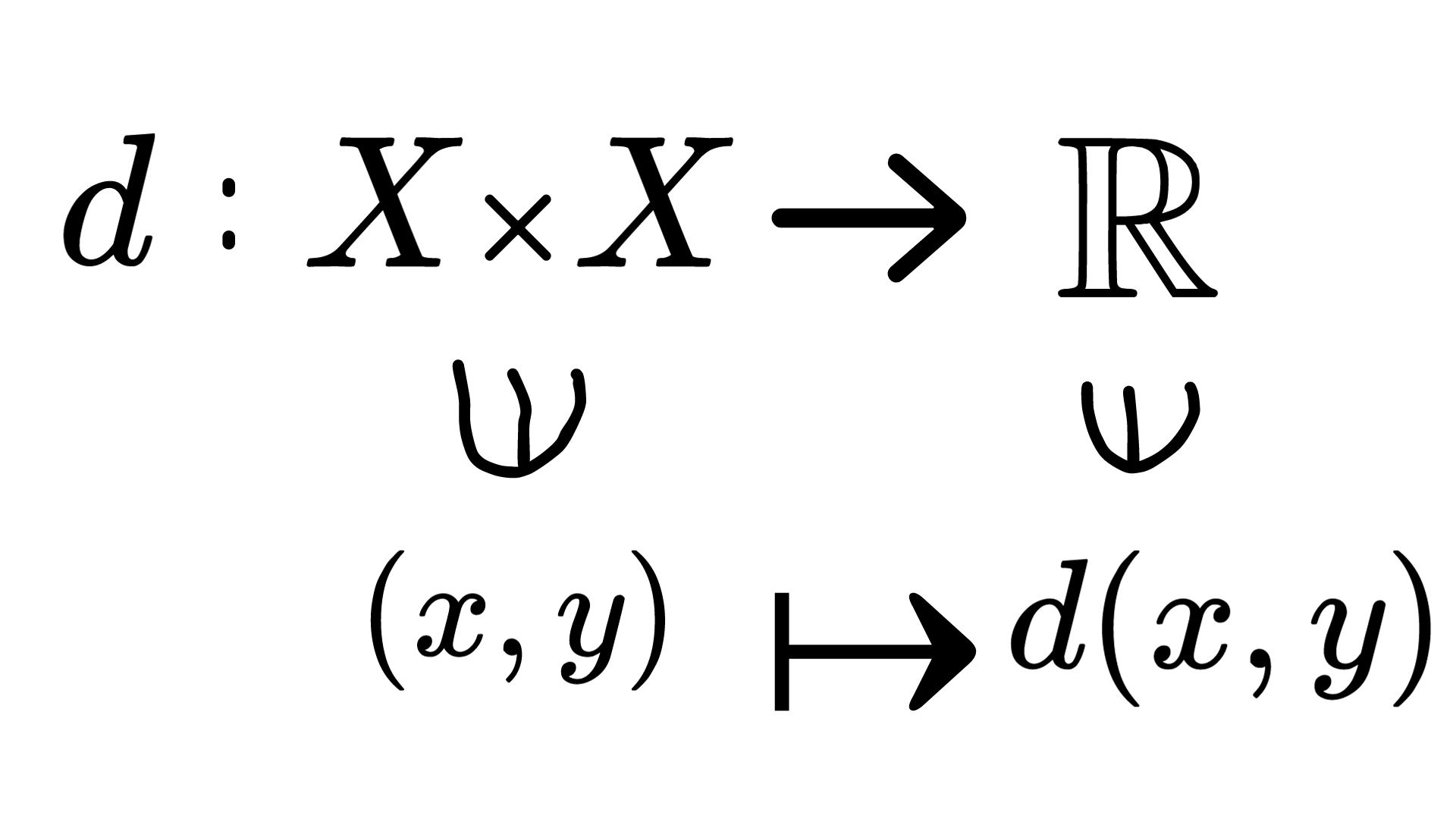
が以下の条件(ⅰ)～(ⅲ)を満たすとき \(d\) を \(X\) 上の距離関数という

(ⅰ)\(\forall x, y \in Xに対し、d(x,y)\geq 0, また、d(x,y)=0となるのはx=yのみ\)
(ⅱ)\(\forall x,y \in Xに対し、d(x,y)=d(y,x)\) \((対称律)\)
(ⅲ)\(\forall x,y \in Xに対し、d(x,z)\leq d(x,y)+d(y,z)\) \((三角不等式)\)

そして、この組 \((X,d)\) を距離空間と呼ぶ

一般の集合\(X\)を考えるとき、上記の(ⅰ)～(ⅲ)の条件を満たすとユークリッド距離空間のときと同様に距離について定義することが出来、一般の集合で距離を考えることが出来るようになります。

では、距離空間を定義したので、距離空間上で考えれる、収束や連続についての定義を考えて行きます。

これは、距離空間上での定義なのでそれを踏まえて考えていきましょう。

1-3.距離空間上での収束の定義

定義

\((X,d):距離空間\)
\(\{ x_{k} \}_{k=1}^\infty:Xの点列\) \((x_{k}\in X)\)

\((1)\{ x_{k} \}_{k=1}^\inftyがx\in X\)に収束するとは、

「\(\forall \varepsilon \gt 0, \exists N \gt 0, \forall k \geq N, d(x_{k},x) \lt \varepsilon\)」が成り立つこと

\((2)\{ x_{k} \}_{k=1}^\infty\)がコーシー列とは、

「\(\forall \varepsilon \gt 0, \exists N \gt 0, \forall n,m \geq N, d(x_{k},x)\lt \varepsilon\)」が成り立つこと

1-4.距離空間上での連続の定義

定義

\((X_1, d_1),\) \((X_2, d_2):距離空間\)

写像 \(f:X_1 \longrightarrow X_2\)

\((1)fがa\in X_1で(d_1,d_2に関して)\)連続であるとは、

「\(\forall \varepsilon \gt 0, \exists \delta \gt 0, d_1(x,a) \lt \deltaとなる\forall x \in X_1はd_2(f(x),f(a)) \lt \varepsilon\)」が成り立つこと

\((2)\)\(fが\forall a \in X_1で連続なとき、fはX_1上で連続という\)

では距離空間上の収束、連続の定義を踏まえた例題を今から解いていきましょう。

1-5.距離空間の基本的な例

例

\(\mathbb{R}^n上で考える.\)

\(x=(x_1,x_2,・・・,x_n) \in \mathbb{R}^n\)に対し、
\(|x|=\sqrt{x_1^2+x_2^2+・・・+x_n^2}\)
\(|x|_0:=|x_1|+・・・+|x_n|\)
\(|x|_1:=max\{ |x_1|,・・・,|x_n| \}\)と定めたとき、

\(x=(3,4)\)とすると、
\(|x|_1=5\)
\(|x|_0=|3|+|4|=3\)
\(|x|_1=max\{ |3|,|4| \}=4\)

と同じユークリッド距離空間内の距離でも異なる数になるような距離関数を定義することが出来る